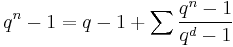Wedderburn's little theorem
In mathematics, Wedderburn's little theorem states that every finite domain is a field. In other words, for finite rings, there is no distinction between domains, skew-fields and fields.
The Artin–Zorn theorem generalizes the theorem to alternative rings.
Contents |
History
The original proof was given by Joseph Wedderburn in 1905,[1] who went on to prove it two other ways. Another proof was given by Leonard Eugene Dickson shortly after Wedderburn's original proof, and Dickson acknowledged Wedderburn's priority. However, as noted in (Parshall 1983), Wedderburn's first proof was incorrect – it had a gap – and his subsequent proofs came after he had read Dickson's correct proof. On this basis, Parshall argues that Dickson should be credited with the first correct proof.
A simplified version of the proof was later given by Ernst Witt.[1] Witt's proof is sketched below. Alternatively, the theorem is a consequence of the Skolem–Noether theorem.
Sketch of proof
Let  be a finite domain. For each nonzero
be a finite domain. For each nonzero 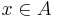 , the map
, the map
is injective; thus, surjective. Hence,  has a left inverse. By the same argument,
has a left inverse. By the same argument,  has a right inverse. A is thus a skew-field. Since the center
has a right inverse. A is thus a skew-field. Since the center 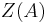 of
of  is a field,
is a field,  is a vector space over
is a vector space over 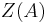 with finite dimension n. Our objective is then to show
with finite dimension n. Our objective is then to show 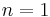 . If
. If  is the order of
is the order of 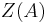 , then A has order
, then A has order 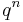 . For each
. For each 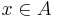 that is not in the center, the centralizer
that is not in the center, the centralizer 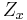 of x has order
of x has order 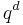 where d divides n. Viewing
where d divides n. Viewing 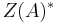 ,
, 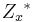 and
and 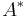 as groups under multiplication, we can write the class equation
as groups under multiplication, we can write the class equation
where the sum is taken over all representatives  that is not in
that is not in 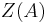 and d are the numbers discussed above.
and d are the numbers discussed above. 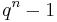 and
and 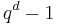 both admit factorization in terms of cyclotomic polynomials
both admit factorization in terms of cyclotomic polynomials 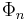 . After cancellation, we see that
. After cancellation, we see that 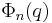 divides
divides 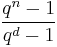 and
and 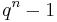 , so it must divide
, so it must divide 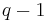 . So we reach contradiction unless
. So we reach contradiction unless 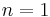 .
.
Notes
References
- Parshall, K. H. (1983), In pursuit of the finite division algebra theorem and beyond: Joseph H M Wedderburn, Leonard Dickson, and Oswald Veblen, Archives of International History of Science, 33, pp. 274–99
- Lam, Tsit-Yuen (2001). A first course in noncommutative rings. Graduate texts in mathematics. 131 (2 ed.). Springer. ISBN 0387951830.